soccerfreakjj10
Rock Star
Silver Level
As I was just busted out of a tournament on the button trying to steal the huge blinds of a turbo tournament, I screamed to myself "OF THE COURSE HE PICKS UP #$%$ING POCKET JACKS IN THE BB."
This isn't the first time i have been busted out of a tournament pushing all in from the button to steal the blinds. It seems to happen a lot.
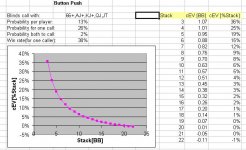
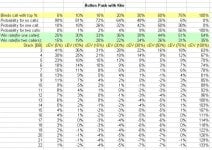
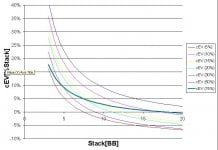
I do feel i made a mistake in this hand (because i am out), but I am curious if anybody knows or is smart enough to calculate the odds that a blind picks up a hand worth calling a push from the button (chip stacks being close enough that a call would be a big chunk of a blinds chips .) I would say those hands would be pocket 6s-As, AK AQ KQ AJ maybe even KJ, QJ, and J10. I bet if somebody figured this out then I would be surprised by the likelihood and try to steal like this far less...
I am still steaming and shocked i didn't just fold and wait for at least an ace to put my chips in with. As you can see though the blinds were huge and i believe my M was at 2.5 - deep in the red zone - so is this the right play in the situation?
here is the example i refer to:
full tilt poker Game #4250123462: Satellite to $15K Guarantee (31678638), Table 4 - 200/400 Ante 50 - No Limit Hold'em - 14:37:14 ET - 2007/11/21
Seat 1: backword (3,515)
Seat 2: Niarn85 (3,065)
Seat 3: Rounder63 (1,943)
Seat 4: goldog (4,500)
Seat 5: soccerfreakjj10 (2,745)
Seat 7: Bearhunter 11 (8,165)
Seat 8: sHuller (2,760)
Seat 9: brejne (1,895)
backword antes 50
Niarn85 antes 50
Rounder63 antes 50
goldog antes 50
soccerfreakjj10 antes 50
Bearhunter 11 antes 50
sHuller antes 50
brejne antes 50
Bearhunter 11 posts the small blind of 200
sHuller posts the big blind of 400
The button is in seat #5
*** HOLE CARDS ***
Dealt to soccerfreakjj10 [6s Kd]
brejne folds
backword folds
Niarn85 folds
Rounder63 folds
goldog folds
soccerfreakjj10 raises to 2,695, and is all in
Bearhunter 11 folds
sHuller calls 2,295
soccerfreakjj10 shows [6s Kd]
sHuller shows [Js Jc]
*** FLOP *** [Qs 6h 7s]
*** TURN *** [Qs 6h 7s] 7♥
*** RIVER *** [Qs 6h 7s 7h] Q♦
soccerfreakjj10 shows two pair, Queens and Sevens
sHuller shows two pair, Queens and Jacks
sHuller wins the pot (5,990) with two pair, Queens and Jacks
soccerfreakjj10 stands up
This isn't the first time i have been busted out of a tournament pushing all in from the button to steal the blinds. It seems to happen a lot.
I do feel i made a mistake in this hand (because i am out), but I am curious if anybody knows or is smart enough to calculate the odds that a blind picks up a hand worth calling a push from the button (chip stacks being close enough that a call would be a big chunk of a blinds chips .) I would say those hands would be pocket 6s-As, AK AQ KQ AJ maybe even KJ, QJ, and J10. I bet if somebody figured this out then I would be surprised by the likelihood and try to steal like this far less...
I am still steaming and shocked i didn't just fold and wait for at least an ace to put my chips in with. As you can see though the blinds were huge and i believe my M was at 2.5 - deep in the red zone - so is this the right play in the situation?
here is the example i refer to:
full tilt poker Game #4250123462: Satellite to $15K Guarantee (31678638), Table 4 - 200/400 Ante 50 - No Limit Hold'em - 14:37:14 ET - 2007/11/21
Seat 1: backword (3,515)
Seat 2: Niarn85 (3,065)
Seat 3: Rounder63 (1,943)
Seat 4: goldog (4,500)
Seat 5: soccerfreakjj10 (2,745)
Seat 7: Bearhunter 11 (8,165)
Seat 8: sHuller (2,760)
Seat 9: brejne (1,895)
backword antes 50
Niarn85 antes 50
Rounder63 antes 50
goldog antes 50
soccerfreakjj10 antes 50
Bearhunter 11 antes 50
sHuller antes 50
brejne antes 50
Bearhunter 11 posts the small blind of 200
sHuller posts the big blind of 400
The button is in seat #5
*** HOLE CARDS ***
Dealt to soccerfreakjj10 [6s Kd]
brejne folds
backword folds
Niarn85 folds
Rounder63 folds
goldog folds
soccerfreakjj10 raises to 2,695, and is all in
Bearhunter 11 folds
sHuller calls 2,295
soccerfreakjj10 shows [6s Kd]
sHuller shows [Js Jc]
*** FLOP *** [Qs 6h 7s]
*** TURN *** [Qs 6h 7s] 7♥
*** RIVER *** [Qs 6h 7s 7h] Q♦
soccerfreakjj10 shows two pair, Queens and Sevens
sHuller shows two pair, Queens and Jacks
sHuller wins the pot (5,990) with two pair, Queens and Jacks
soccerfreakjj10 stands up