Poker Odds for Dummies
 Reviewed by WSOP Winner Chris ‘Fox’ Wallace
Reviewed by WSOP Winner Chris ‘Fox’ WallaceBeginner-friendly
14 minute read
This poker odds guide is for you if:
- You have a basic knowledge of poker.
- You want to improve your understanding of how Texas Hold’em poker odds work.
This short, practical guide will show you how to calculate poker odds and pot odds like the best poker players so you can gain the upper hand on both physical and online tables.
Need some quick help? Check out our handy Texas Hold’em poker cheat sheet, which simply tells you which poker hands you should play when based on poker odds.
What are pot odds and poker outs?
See more free video tutorial content from our poker school:
Become a winning poker player in 30 days
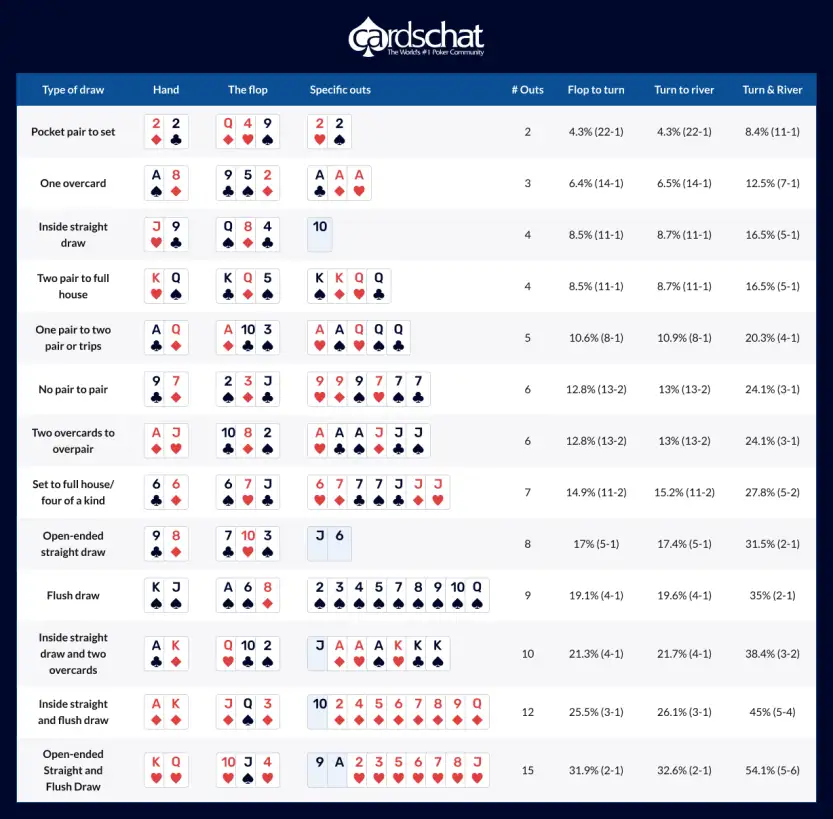
Poker odds chart
Drawing to improve your hand is an essential part of poker, but the difference between winning and losing often comes down to knowing when you’re getting the right price to call to try and hit your card. This chart shows the most common drawing situations you’ll find yourself in, as well as how much needs to be in the pot already to make it worth calling.
We’d recommend bookmarking this page so you can refer to these poker cheat sheets next time you face a tricky call online.
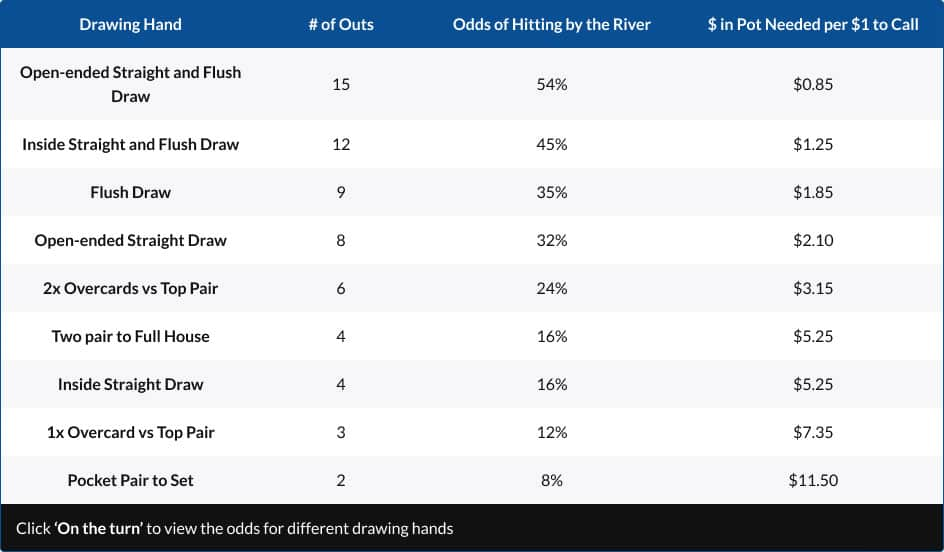
On the flop
| Drawing Hand | # of Outs | Odds of Hitting by the River | $ in Pot Needed per $1 to Call |
|---|---|---|---|
| Open-ended Straight and Flush Draw | 15 | 54% | $0.85 |
| Inside Straight and Flush Draw | 12 | 45% | $1.25 |
| Flush Draw | 9 | 35% | $1.85 |
| Open-ended Straight Draw | 8 | 32% | $2.10 |
| 2x Overcards vs Top Pair | 6 | 24% | $3.15 |
| Two pair to Full House | 4 | 16% | $5.25 |
| Inside Straight Draw | 4 | 16% | $5.25 |
| 1x Overcard vs Top Pair | 3 | 12% | $7.35 |
| Pocket Pair to Set | 2 | 8% | $11.50 |
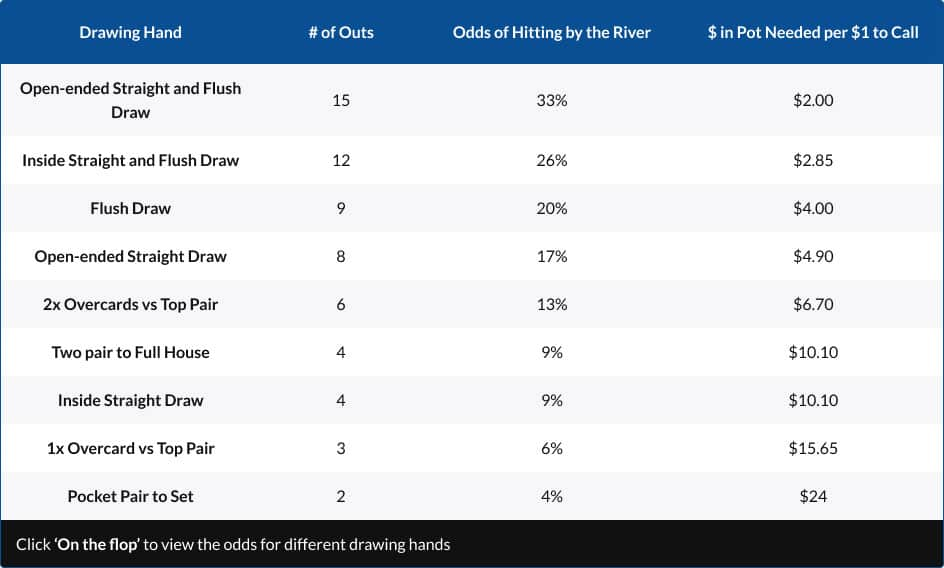
On the turn
| Drawing Hand | # of Outs | Odds of Hitting by the River | $ in Pot Needed per $1 to Call |
|---|---|---|---|
| Open-ended Straight and Flush Draw | 15 | 33% | $2.00 |
| Inside Straight and Flush Draw | 12 | 26% | $2.85 |
| Flush Draw | 9 | 20% | $4.00 |
| Open-ended Straight Draw | 8 | 17% | $4.90 |
| 2x Overcards vs Top Pair | 6 | 13% | $6.70 |
| Two pair to Full House | 4 | 9% | $10.10 |
| Inside Straight Draw | 4 | 9% | $10.10 |
| 1x Overcard vs Top Pair | 3 | 6% | $15.65 |
| Pocket Pair to Set | 2 | 4% | $24.00 |
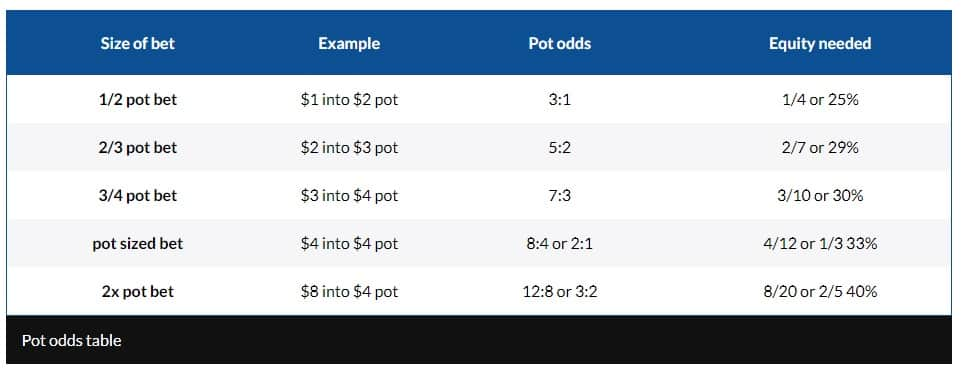
Pot odds table
And here’s our at-a-glance guide to poker pot odds, using some of the more common bet sizes you’re likely to face at the table. Want some guidance on what you should be playing in the first place? We recommend checking our starting hands page for more information.
| Size of bet | Example | Pot odds | Equity needed |
|---|---|---|---|
| 1/2 pot bet | $1 into $2 pot | 3:1 | 1/4 or 25% |
| 2/3 pot bet | $2 into $3 pot | 5:2 | 2/7 or 29% |
| 3/4 pot bet | $3 into $4 pot | 7:3 | 3/10 or 30% |
| pot sized bet | $4 into $4 pot | 8:4 or 2:1 | 4/12 or 1/3 33% |
| 2x pot bet | $8 into $4 pot | 12:8 or 3:2 | 8/20 or 2/5 40% |
PART 1
How odds work
Let’s say you’re betting on a horse race and are given odds of ‘seven to one’, it will be written ‘7:1’. This means that for every $1 you bet you’ll get paid $7 if you win. So if you bet $10 at 7:1 you’ll win $70 (plus your stake).
7:1
Odds
=
$70
Winnings from a $10 bet
When the odds are particularly high against you winning, it’ll often be referred to as the ‘long shot’, which generally means it has only the slightest chance of succeeding.
Higher odds generally mean you have less chance of winning. If someone offers you odds of 100:1 it means they’re convinced you’re not going to win.
PART 2
Poker odds tell you the probability of hitting any given card
Before we can get into a discussion of poker odds while playing poker online, you need to know how to calculate your ‘outs’. Outs are simply the cards that will help you improve your hand and make it better than what you think your opponent is holding.
To calculate odds you first need the number of winning cards, or ‘outs’
Opponent’s hand is unknown:
Ignore your opponent’s hand
Your hand is dealt:
To make a flush
you will need 3 more hearts
The dealer lays out:
4
hearts now visible
To win you’ll need any heart:
9
out of 13 hearts still available. You have 9 ‘outs’
PART 3
Using the ‘outs’ to calculate Texas Hold’em poker odds
Let’s break this down:
- We have already determined that you have nine ‘outs’.
- There are 52 cards in a deck and two of those are in your hand, leaving 50.
- There are four cards exposed from the flop and turn, leaving 46 cards.
- Your opponent is holding two cards, but we ignore those as our calculations in online Texas Hold’em poker are only based on the cards you can see and what could be left in the deck.
First calculate how many cards from the deck you can’t see:
52
Cards in a deck
–
2
Cards in your hand
–
4
Cards dealt in the flop and turn
=
46
Unseen cards
*Still ignoring what your opponent may be holding
The unseen cards are then split into winners and losers:
LOSERS
37 cards in the deck that will cause you to lose
Clubs
Diamonds
Spades
WINNERS
9 cards in the deck that will give you a win
YOUR ODDS
37 to 9
Your odds of getting the winning flush
This simplifies down to
4:1
(or 20% for those that like to use percentages)
In other words, you are 4 times more likely to lose this pot than you are to win it.
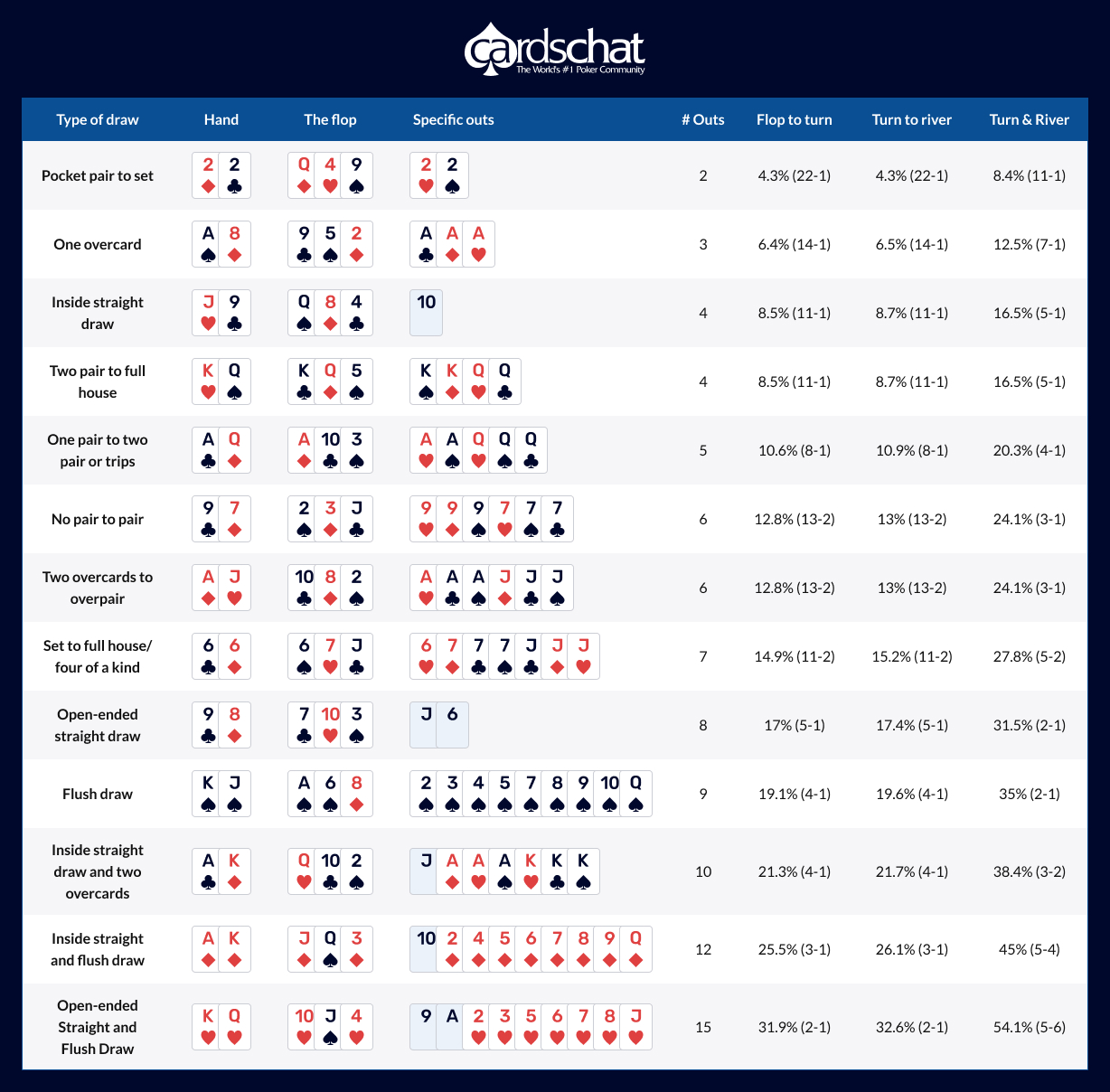
Common poker outs scenarios
To help you get to grips with the idea of poker outs, we’ve provided the outs and odds on some common scenarios you’re likely to see at the table. Use this simple odds chart for calculating odds and probabilities while playing, especially when you are drawing and hoping to improve your hand.
It has basic hand odds given the number of “outs” after the flop or after the turn. These “outs” represent the cards you need to hit to make a better hand, such as turning a pair into three-of-a-kind, or filling a straight draw. You’ll notice there’s a big difference between having just one card to come, and two. For the example above – the flush draw – your chances go up to 35% from 20% if you have both turn and river to come.
If you would like to start practicing or playing, check out our freerolls page for the best poker rooms to get you started, or try our no-risk, no deposit, no download tables to play for free right now!
Poker Odds Chart Download PDF

Poker Odds Chart Download PDF
Feel free to save our poker odds chart image or poker odds chart PDF for use anytime you need it – or bookmark the page!
PART 4
The BIG question – should you call the bet?
So, on the turn you have odds of around 4:1 to win this hand. As to whether you should call your opponent’s bet, that depends on how much money is in the pot. No, that doesn’t mean if there’s a big pot of money you should just go for it. What you should be looking for is the ratio of money you could win compared to the size of your opponent’s bet.
Let’s continue with our example:
- Let’s say there was $90 in the pot and your opponent bets $10.
- That makes a total of $100 in the middle of the table waiting to be won.
- You need to match your opponent’s bet of $10 to see the river card, so it’s going to cost you $10 to see if that last card is going to be one of the nine you need to win.
Step 1: Work out how much you’d normally win from your actual poker odds:
4:1
Odds you actually have of winning the hand
$10
Your bet
=
$40
Money you’d normally win
Step 2: Calculate how much money you could win and the odds you’re getting:
$90
Money in the pot
+
$10
Your rival’s new bet (you must match this bet to continue the game)
=
$100
Money you could win
10
If you match your opponent’s bet and win, you’ll make $10 for every $1 bet. That’s pot odds of 10 to 1.
Step 3: Decide whether to call the bet:
In this example by betting $10 your opponent has effectively given you odds of 10:1, when your actual chance of winning is 4:1. This is like a bookmaker giving you 10:1 odds on a horse that has a 4:1 chance of winning.
Should you call that bet? Yes!
Why? Because the odds are offering you the chance to enjoy a great pay day.
PART 5
But what if I lose?
Even if you make that call, you might still lose. It happens. Remember, your calculated odds were 4:1, meaning you will lose four times for every time you win. That’s why it’s important you are being offered at least the chance to win four times as much as your bet, because statistically in the long run you’ll break even. More importantly, if you are being offered the chance to win more than four times your bet for a 4:1 risk, you’ll eventually make money.
To summarize everything we have calculated so far:
In summary
4:1 are the odds you actually have of winning the hand
This means you can expect to lose 4 hands for every hand you win
10:1 are the odds you’re being offered to call your opponent’s bet
This means you’ll win $100 from a $10 bet
If this situation came up 5 times during the game, and went exactly as the probabilities suggest, it would look like this:
$100
Won from the 1 flush
–
$40
Losses from 4 losing hands
=
$60
Profit from 5 hands
PART 6
A lot to remember? Here’s a handy shortcut: The Rule of 4 and 2
Now that you have worked through the math and seen the theory, it’s time to introduce a handy shortcut. This will help you calculate your chances of winning a hand within the short period of time that online poker allows you to make a decision.
Let’s use our example from step 1:
-
After the flop (first three cards the dealer puts on the table), calculate the number of outs left in the deck:
Using our example from step 1 we had: 9 outs
-
Then simply multiply the number of outs by 4 to get the approximate chance of being dealt a winning card on the turn or river:
9 x 4 = 36%
-
After the turn (fourth card dealt on the table), multiply the number of outs by 2 to give the chance of winning on the river:
9 x 2 = 18%
While this method is not super precise, it provides a clear enough guide when calculating odds in online poker. Once you’ve got the hang of playing poker you may want to start calculating the exact percentage, but for now the rule of 4 and 2 is more than enough to get you started.
You can always use our poker cheat sheet and poker odds calculator when you’re reviewing your poker hands and brushing up on your skills.

Cheat sheets
Our poker odds cheat sheets can give you the edge at the tables and help you make better decisions – especially when you have a drawing hand. Click to download and print them out (or simply bookmark this page) so you always have them handy.
DOWNLOAD IMAGE
DOWNLOAD IMAGE
DOWNLOAD IMAGE
DOWNLOAD IMAGE
Play Texas Hold’em for free at our no-risk practice tables! No downloads, deposits or accounts needed.
Poker Odds FAQ
How do I calculate poker odds?
1) Count the ‘outs’ that would win you the pot, 2) count the number of unseen cards in the deck, 3) subtract the number of outs (A) from the unseen cards, and count the remaining unseen cards (B).
Your odds of winning the hand are therefore (B):(A).
You can always use our handy poker cheat sheet as a guide. It can also help to memorize odds for common situations, for example, knowing that a small pair against two overcards before the flop is roughly 50/50 and that a small pair against a big pair is a 4/1 underdog, etc.
Other odds calculations require more effort and practice. It’s best to routinely use a poker odds calculator to check what your odds were after the fact, you can then adjust your play based on this information in future on similar hands.
How should I calculate odds in my head quickly?
The rule of 4 and 2 is the easiest way to know roughly what your odds of winning your hand are.
It’s a simple process: first work out how many cards you can hit to improve your hand (outs). For example, if you have a flush draw, there are nine cards you can hit to make a flush.
To know the odds of making your flush from the flop, simply multiply your outs by four. If the turn doesn’t bring your card, multiply your outs by two. In this case, on the flop, you have a roughly 36% chance of making your flush by the river (reduced to around 18% on the turn).
How to calculate pre-flop poker odds?
The best way to calculate precise pre-flop odds is to use a dedicated poker odds calculator. However, here are a few quick tricks to know rough odds on the go:
- A pocket pair against two overcards (e.g. 66 vs AQ) is roughly 50/50
- A smaller pair against a bigger pair (e.g. 66 vs AA) is a 4/1 underdog
- Two high cards against two lower cards (e.g. AK v QJ) is roughly 60/40
- A “dominated” hand (e.g. AK v AJ) is a 3/1 underdog
What are pot odds?
Pot odds refers to the price of calling a bet relative to the size of the pot. For example, if the pot is $100 and your opponent bets $100, then you must call $100 to win $200 (their bet plus the pot). This means you’re getting pot odds of $200 to $100, or 2/1.
How do you calculate poker pot odds?
To calculate poker odds, you’ll first need to know your outs. Outs are the cards that can improve your hand. There are many ways to calculate pot odds but here’s a simple way. Rather than using a formula, poker players use the rule of 4 and 2.
The rule says that if you have two cards to come (i.e. on the flop), you can multiply the number of outs you have by four and you’ll come to an approximate percentage of making your hand. If you have only one card to come, on the turn, you can multiply your outs by two to reach an estimated percentage.
To calculate pot odds, determine the amount of chips already in the pot vs the amount you must put in to call. This ratio is an expression of your pot odds.
What are good odds?
Good odds simply means that the pot odds are longer than the odds of making your hand. For example, if you have a flush draw and face an all-in bet on the flop, you will have a roughly 36% chance of making your flush and winning. 36% is a little better than 2:1, so if you have to call a bet of $150 to win $300 or more, you’re getting good odds and should call.
What are the odds of flopping a set?
If you have a pocket pair, you will flop a set roughly one time in nine.
What are the odds of flopping a flush?
If you have two suited cards, you will flop a flush roughly one time in 118. You’ll flop a flush draw around one in 10 times.
What are the odds of being dealt pocket aces?
On average, you’ll be dealt pocket aces once every 220 hands.
What are the odds of winning poker?
Some common poker hand odds to try and remember, assuming just one more card to come, are open-ended straight draws at 4.8:1, four to a flush at 4.1:1, inside straight draw (belly buster) at 10.5:1, one pair drawing to two pairs or trips at 8.2:1, overcards on a ragged board on the turn at 6.7:1, and drawing to a set at 22:1.
How do the odds change with more players?
The more players that are involved in the hand, the lower your chances of winning the pot – even if you’re a favorite. For example, the most powerful starting Hold’em hand is pocket aces. If you’re up against a random hand, you’ll be a huge 85% favorite. If you’re up against five random hands, you’ll still be a huge favorite, but you’ll only win the pot 49% of the time on average.
On top of that, the more players in the pot, the higher the chances that they hold some of your outs. If two players have flush draws, they only have seven outs (not nine) to hit their flush and one of them might lose a big pot!
How many different hands are possible in Texas Hold’em?
If you do not distinguish between suits (which are not ranked in most poker games), then there are 169 different starting hands in Texas Hold’em. The best is A-A and the worst is either 7-2 or 3-2 unsuited, but many other Hold’em hands are considered largely unplayable. If you do differentiate between suits, there are 1,326 possible combinations of two cards. Visit our Texas Hold’em starting hands page for more detailed help.
What are outs in poker?
‘Outs’ is simply the technical term for the cards that can make you the winning hand. For example, if you have Ah-Qh against Jc-Jd on a flop of 8h-5h-2c, you can win with any heart, Queen or Ace for a total of 15 outs.
How do you count outs in poker?
An out is simply a card that will help you win. Look at this example:
If you’re planning on winning with a flush and you have four spades, then there will be nine spades left in the deck. So, you can win with any of these nine spades.
There are thirteen cards in a suit, so you can easily calculate that because you have four spades there will be nine left (13 – 4 = 9).
What are the chances of winning with pocket aces?
Pocket aces are a solid hand that give you a good chance of winning. Your odds of winning depend on the number of people playing, but generally is at a minimum of 25% if each player stays in until the end, and the odds go up as each player drops out of the hand. Learn how to protect your strong hands to prevent worse ones from out-drawing you, and you’ll win more with your premium hands!
What is the percentage of hitting a set on the flop?
The approximate probability of hitting a set on the flop is 12% which isn’t too bad, but certainly nothing that you want to rely on while playing the game. ‘Set-mining’ is the act of calling a bet with a small pair, hoping to hit three-of-a-kind on the flop for a very strong, yet dangerously concealed hand. Given the low chances of success, however, this should only be attempted if your stack is big enough – and the bet you’re facing is small enough – that you won’t suffer too badly if you don’t hit your card.
Looking to level up your Poker Skills further?