zachvac
Legend
Silver Level
so I'm sitting in an econ class, the easiest class ever, yet the "professor" teaches it like it's a middle school class. She literally lectures directly from the book, yet attendance is mandatory and we are not allowed to use laptops at all. So I'm not going to focus entirely on this class, because as mentioned it's the easiest class ever, so I figure, how about some poker calculations. I don't even know why I did these, but I got some interesting results.
Firstly, pot odds. Even sum (no rake)
If you are the underdog, to call any bet you want to win at least your bet back on average. Let E = chance of winning (I was thinking ev but that's actually EX), X = pot size before bet, B = bet.
E(X + 2B) > B
We'll calculate when they're equal first
EX + 2EB = B
B - 2EB = EX
B = EX/(1 - 2E)
if you're a favorite you want to be betting enough that you are getting at least the pot and your bet back, because if you bet your entire stack (assuming it's large enough to induce a fold), that's what you would get.
E(X + 2B) > X + B
Again, calculate equality
EX + 2EB = X + B
B - 2EB = EX - X
B = (-EX + X)/(-1 + 2E)
So now you're thinking "great, I can do these calculations without a formula like this, what use is that?". Well I'm so glad you asked. Let's graph these.
In the graphs, we set X = 1 (so bet is in proportion to size of pot. B = 1 is a pot sized bet, B = 1/2 is 1/2 pot size, etc.) and E=X (because that's what we really want anyway). So...
Underdog:
B = X/(1 - 2X)
Favorite:
B = (1 - X)/(-1 + 2X)
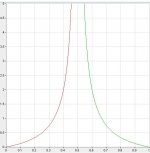
First image below is both of these graphs. Left half is 1st one and right half is 2nd. Note that these are exactly symmetrical. That's because in a 0 sum game, if there is a 75-25 situation, the bet that is even money for the underdog is also even money for the favorite. But the much more important graph is the graph of the left half and the right half reflected about the line x = 0.5. This graph would give us 2 lines, one line or the underdog (the one graphed already) and one line for the favorite (the one reflected). The favorite wants to bet above that line while the underdog wants to bet below that line. Note that both of these conditions can never be satisfied although with rake it is possible that neither of these conditions are satisfied. I'm not going to graph that with no rake because it would simply be the left half with another graph right on top of it. So what does this mean? It means that if you can make your opponent make a slight mistake (favorite bet below the curve or underdog call something above the curve), it always equates in a profit for you.
Now let's do some calculations with rake. Now rake is usually in discrete amounts (5 cents for every dollar usually), but we're going to ignore that and pretend that rake is always the same amount percentage-wise (this also means no cap). Now our calculations are slightly more complex. I'm not going to do them here but I'll summarize here:
Underdog:
E(1-R)(X+2B) = B
leads to...
B = (EX - ERX)/(1 - 2E - 2ER)
Favorite:
E(1-R)(X+2B) = B+RX
leads to...
B = (EX - EXR - X + RX)/(1 - 2E + 2ER)
Substitute X = 1, E = X again
Underdog:
B = (X - RX)/(1 - 2X - 2RX)
Favorite:
B = (X - RX - 1 + R)/(1 - 2X + 2RX)
pointless again without a graph. We're not going to graph this though, as this would be relatively worthless. The more important graph is the underdog graph as well as the graph of the favorite reflected about x=0.5 (which is amount they must bet over if they're opponent has probability x of winning, which is always < 0.5 because they're a favorite).
So we graph the underdog equation as well as the favorite equation translated. The translation will be F(-x + 1)
B = ((1-X) - R(1-X) - 1 + R)/(1 - 2(1-X) + 2R(1-X))
Great, so let's graph the 2 and we can use R = 0.05 which is the norm for most sites I think.
B = ((1 - x) - 0.05(1 - x) - 1 + 0.05)/(1 - 2(1 - x) + 2*0.05*(1 - x))
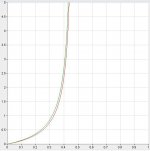
This is the second graph, and note that for a bet to be profitable the underdog needs a bet under the red curve and the favorite needs a bet over the green curve. If the bet is in between there neither person is getting a profitable proposition because of rake.
Now comes the fun part. To be profitable, how bad of a mistake does an opponent have to make. Obviously with rake if no one made mistakes and played hands face up everyone would lose. So if the hands were played face up and you played every hand perfectly, how bad of a mistake would an opponent have to make for you to profit? Well that's tough to quantify. I'm just thinking aloud here, but how about we quantify size of mistake as amount of extra money they will pay divided by bet size. This graph is already scaled by pot size, so we already don't have to worry about the units, so let's see what kind of mistake we need. Let's leave the r in just for kicks so we can do this for any rake r.
(((1 - x) - 0.05(1 - x) - 1 + 0.05)/(1 - 2(1 - x) + 2*0.05*(1 - x)) - (x - 0.05x)/(1 - 2x - 2*0.05*x))/(((1 - x) - 0.05(1 - x) - 1 + 0.05)/(1 - 2(1 - x) + 2*0.05*(1 - x)))
I'm not showing the work here, but with the R inserted, this simplifies down to:
(2R - 4RX)/(1 - 2X - 2R + 2RX)
This is how bad of a mistake they have to make for it to be profitable for you. If this number is 1 it means they have to call a bet of twice what would be profitable for them for it to be profitable for you, and so on and so forth.
The last graph is a graph of error, for how close a decision is. Note that as the edge gets closer to 0, it gets to the point where they need to make a huge mistake. A better mistake calculations I guess would be how much they lose by making that decision, but I'll save that for another day.
The important thing to note in that graph is that the mistake they need to make is a little under 0.15. So say you're playing $25nl (just easier for me to get an example), someone has a flush draw against you, the odds of hitting (X in the graphs) are 9/47. With the rake, they need 171/562=0.304*pot to have odds. With say a $2.50 pot (standard raise and call preflop), they could call a 76 cent bet and have odds. But since they need to make around an 0.15 mistake, they must pay ~87 cents to give you odds.
So you see this isn't terrible, but let's see what happens when you increase the rake. Make it 15%. All of a sudden they need less than 73 cents and you need more than $1.09. They must make a horrible mistake for you to profit. No particularly interesting conclusions, just showing how although current online is reasonable and possible to profit, raise the rake much more (10% gives 75 cents and 95 cents) and you need to have dumber and dumber opponents. Not sure of the normal rake but I've heard of live rakes being 10% and when you factor in dealer tips that rake can be pretty high. Anyway I thought I was going to be able to conclude something amazing from this but apparently not really. But I was able to quantify the kind of mistakes opponents have to make (they get very high for close to even money decisions, I tried to find that inflection point where the derivative = 1, that got way too tough to do by hand, you could do it on a calculator for each given r, but it's close enough to 0.5 with any reasonable rake that it really doesn't matter that much) as well as a formula for what kind of odds you need to have/give for a play to be profitable, given a probability, the rake, and the pot size. Sorry if you felt I just wasted your time with useless calculations.
Firstly, pot odds. Even sum (no rake)
If you are the underdog, to call any bet you want to win at least your bet back on average. Let E = chance of winning (I was thinking ev but that's actually EX), X = pot size before bet, B = bet.
E(X + 2B) > B
We'll calculate when they're equal first
EX + 2EB = B
B - 2EB = EX
B = EX/(1 - 2E)
if you're a favorite you want to be betting enough that you are getting at least the pot and your bet back, because if you bet your entire stack (assuming it's large enough to induce a fold), that's what you would get.
E(X + 2B) > X + B
Again, calculate equality
EX + 2EB = X + B
B - 2EB = EX - X
B = (-EX + X)/(-1 + 2E)
So now you're thinking "great, I can do these calculations without a formula like this, what use is that?". Well I'm so glad you asked. Let's graph these.
In the graphs, we set X = 1 (so bet is in proportion to size of pot. B = 1 is a pot sized bet, B = 1/2 is 1/2 pot size, etc.) and E=X (because that's what we really want anyway). So...
Underdog:
B = X/(1 - 2X)
Favorite:
B = (1 - X)/(-1 + 2X)
First image below is both of these graphs. Left half is 1st one and right half is 2nd. Note that these are exactly symmetrical. That's because in a 0 sum game, if there is a 75-25 situation, the bet that is even money for the underdog is also even money for the favorite. But the much more important graph is the graph of the left half and the right half reflected about the line x = 0.5. This graph would give us 2 lines, one line or the underdog (the one graphed already) and one line for the favorite (the one reflected). The favorite wants to bet above that line while the underdog wants to bet below that line. Note that both of these conditions can never be satisfied although with rake it is possible that neither of these conditions are satisfied. I'm not going to graph that with no rake because it would simply be the left half with another graph right on top of it. So what does this mean? It means that if you can make your opponent make a slight mistake (favorite bet below the curve or underdog call something above the curve), it always equates in a profit for you.
Now let's do some calculations with rake. Now rake is usually in discrete amounts (5 cents for every dollar usually), but we're going to ignore that and pretend that rake is always the same amount percentage-wise (this also means no cap). Now our calculations are slightly more complex. I'm not going to do them here but I'll summarize here:
Underdog:
E(1-R)(X+2B) = B
leads to...
B = (EX - ERX)/(1 - 2E - 2ER)
Favorite:
E(1-R)(X+2B) = B+RX
leads to...
B = (EX - EXR - X + RX)/(1 - 2E + 2ER)
Substitute X = 1, E = X again
Underdog:
B = (X - RX)/(1 - 2X - 2RX)
Favorite:
B = (X - RX - 1 + R)/(1 - 2X + 2RX)
pointless again without a graph. We're not going to graph this though, as this would be relatively worthless. The more important graph is the underdog graph as well as the graph of the favorite reflected about x=0.5 (which is amount they must bet over if they're opponent has probability x of winning, which is always < 0.5 because they're a favorite).
So we graph the underdog equation as well as the favorite equation translated. The translation will be F(-x + 1)
B = ((1-X) - R(1-X) - 1 + R)/(1 - 2(1-X) + 2R(1-X))
Great, so let's graph the 2 and we can use R = 0.05 which is the norm for most sites I think.
B = ((1 - x) - 0.05(1 - x) - 1 + 0.05)/(1 - 2(1 - x) + 2*0.05*(1 - x))
This is the second graph, and note that for a bet to be profitable the underdog needs a bet under the red curve and the favorite needs a bet over the green curve. If the bet is in between there neither person is getting a profitable proposition because of rake.
Now comes the fun part. To be profitable, how bad of a mistake does an opponent have to make. Obviously with rake if no one made mistakes and played hands face up everyone would lose. So if the hands were played face up and you played every hand perfectly, how bad of a mistake would an opponent have to make for you to profit? Well that's tough to quantify. I'm just thinking aloud here, but how about we quantify size of mistake as amount of extra money they will pay divided by bet size. This graph is already scaled by pot size, so we already don't have to worry about the units, so let's see what kind of mistake we need. Let's leave the r in just for kicks so we can do this for any rake r.
(((1 - x) - 0.05(1 - x) - 1 + 0.05)/(1 - 2(1 - x) + 2*0.05*(1 - x)) - (x - 0.05x)/(1 - 2x - 2*0.05*x))/(((1 - x) - 0.05(1 - x) - 1 + 0.05)/(1 - 2(1 - x) + 2*0.05*(1 - x)))
I'm not showing the work here, but with the R inserted, this simplifies down to:
(2R - 4RX)/(1 - 2X - 2R + 2RX)
This is how bad of a mistake they have to make for it to be profitable for you. If this number is 1 it means they have to call a bet of twice what would be profitable for them for it to be profitable for you, and so on and so forth.
The last graph is a graph of error, for how close a decision is. Note that as the edge gets closer to 0, it gets to the point where they need to make a huge mistake. A better mistake calculations I guess would be how much they lose by making that decision, but I'll save that for another day.
The important thing to note in that graph is that the mistake they need to make is a little under 0.15. So say you're playing $25nl (just easier for me to get an example), someone has a flush draw against you, the odds of hitting (X in the graphs) are 9/47. With the rake, they need 171/562=0.304*pot to have odds. With say a $2.50 pot (standard raise and call preflop), they could call a 76 cent bet and have odds. But since they need to make around an 0.15 mistake, they must pay ~87 cents to give you odds.
So you see this isn't terrible, but let's see what happens when you increase the rake. Make it 15%. All of a sudden they need less than 73 cents and you need more than $1.09. They must make a horrible mistake for you to profit. No particularly interesting conclusions, just showing how although current online is reasonable and possible to profit, raise the rake much more (10% gives 75 cents and 95 cents) and you need to have dumber and dumber opponents. Not sure of the normal rake but I've heard of live rakes being 10% and when you factor in dealer tips that rake can be pretty high. Anyway I thought I was going to be able to conclude something amazing from this but apparently not really. But I was able to quantify the kind of mistakes opponents have to make (they get very high for close to even money decisions, I tried to find that inflection point where the derivative = 1, that got way too tough to do by hand, you could do it on a calculator for each given r, but it's close enough to 0.5 with any reasonable rake that it really doesn't matter that much) as well as a formula for what kind of odds you need to have/give for a play to be profitable, given a probability, the rake, and the pot size. Sorry if you felt I just wasted your time with useless calculations.