Value Expectation

[maybull]

How often do u rely on Value Expectation during your game?

 

[maybull]

...or maybe a better question would be, how important is it to be able to calculate expected value at any given time? Like, do I need to spend some serious time brushing up on my fraction conversions and multiplication so I can I can whip out a value analysis on the fly at any time?

You may have guessed that I'm not really all that strong a arithmetician (think Ed Grimly). I absolutely will take the time to figure it out, study it and make it my friend if I need to. But, if I don't need to, then I'd rather spend time studying other "stuff".

Thoughts?

I've been playing online for a few months now - micro tables only. I do ok, but want to do much much better. I'll do whatever it takes to get better, but I just want to make sure I'm not waisting time. I feel like there is so much to learn.

When I read some of the articles under "Strategy Articles", I notice many of them warn readers to learn/understand value expectation before moving onto pot odds etc. So, I guess I could heed those warnings and just accept that I need to become very familiar with value expectation.

Buuuuut then again, maybe the author was just joking?

lol.

 

[Tammy]

I don't think the author was joking. Knowing expected value (whether + or -), being able to quickly calculate pot odds/implied odds is very important. I'm no mathmetician either, but having an elementary grasp on these concepts can really help you make the right decisions. Check out these articles if you haven't already:

Five Fundamentals of Poker - Poker Theory

Poker: Expected Value
Poker: Pot Odds & Implied Odds
Poker: Position
Poker: Pot Size
Poker: Equity

 

[maybull]

Hey juiceeQ, thanks for replying to my post.

Okay, so it sounds like as long as I have somewhat of a grasp on these concepts I should be OK.

I understand and can calculate pot odds/implied odds, but for some reason when I read the article on the Expected Value I go cross eyed. I'll read and re read until it becomes more familiar.

Thanks again for taking the time to reply

 

[Tammy]

No problem. And I'll tell you a little secret...I get a little cross-eyed too...shhh! Best of luck to you, and I hope you're enjoying the site so far.

 

[maybull]

hahaha...Thanks, I'll keep that one between u and me

 

[Cheetah]

No problem. And I'll tell you a little secret...I get a little cross-eyed too...shhh! Best of luck to you, and I hope you're enjoying the site so far.

hahaha...Thanks, I'll keep that one between u and me

Too late. I caught you!


Let me try to explain what it really is.

Expected Value is really a big name for "Average Value".

Say in a cash game you get involved in races where you have 50% chance to win $100 and 50% chance to lose $100. How much is your average win? Zero! The fancy name is that the Expected Value = 0.

Now let's say that in that game, everytime you race you have a bigger pocket pair than your opponent. That means that you will win 80% of the time and your opponent will win 20% of the time. Again, you are both all-in for $100 each.

In this case, we cannot take a simple average because we win 4 times as more often than our opponent. In the first example, when our chances to win and lose were the same (coin-flip), our Expected Value was zero. Now, it is more than zero. If we play 5 times, we win on average 4 times $100 and we lose 1 time $100. So after 5 times on average we will have $400 - $100 = $300. If we play 10 times, on average we make $600. So how much do we make on average EACH time we play? If we make $600 for ten times, then we make $60 each time. That is called Expected Value which is just how much we make or lose on average.

The formula for Expected Value (EV) is:

EV = (% to win)*$won - (% to lose)*$lost

In the coin flip example, we win $100 50% of the time and lose it 50% of the time, so:

EV(for example 1) = 50% * $100 - 50% * $100 = $0

In the second example, our pair against smaller pair:
% to win = 80%
% to lose = 20%
$won = $100
$lost = $100

EV(for example 2) = 80% * $100 - 20% * $100
= $80 - $20
= $60


Now, is there any relation between expected value and odds? YES!

In the first example, our odds were 50% to win and 50% to lose so the odds were 1:1.

In the second example, we were 80% to win and 20% to lose which gives us 4 to 1 odds. So what are odds (to win or lose)?

Odds(to win) = (% to win)/(% to lose)

Odds(to lose) = (% to lose)/(% to win)

In the examples above, odds to win are:

Odds(to win example 1) = 50%/50% = 1:1
Odds(to win example 2) = 80%/20% = 4:1


So Odds and Expected Value are different ways to talk about the same thing. If you have odds when calling, then your EV is positive, and vice versa, if you don't have odds, your EV is negative.

Sometimes it is more convenient to think in terms of odds. Other times it is more convenient to think in terms of EV.


Let me give a final example to illustrate these 2 concepts:

Let's say that in a cash game you have a flush draw on the flop and someone moves all-in and they have you covered. You want to determine whether you have odds to call. That is the same thing as determining whether the EV of calling is positive.

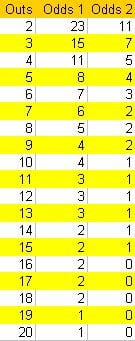
Thinking in terms of odds here is easier. The attached odds table converts outs to required odds for 1 card to come (Odds 1) and 2 cards to come(Odds 2).

In our case, we have 9 outs to make our flush and 2 cards to come. The odds table tells us that the odds AGAINST us are 2:1. So in order to call profitably, the pot odds must be at least 2 to 1.

(A) If the pot is $1,000 and we have to call $1,000, that's only 1:1 pot odds. That will lose us money because we stand to win and lose the same amount, but we will lose twice as often. Than means our EV is negative. That means we must fold.

(B) If the pot is $2,000 and we have to call $1,000, that's 2:1 pot odds. We will now break even. This is the same as saying EV = 0. We can now either fold or call. In the long term, we don't make or lose any money.

(C) If the pot is $3,000 and we have to call $1,000, that's 3:1 pot odds. That will now makes us money. Than means our EV is positive. We should definitly call in this situation.


Now let's calculate the EV for the 3 cases above to illustrate that odds and EV are related.

In all cases, the odds to win are 33% and the odds to lose are 67%. How do I know that? If I substitute in the formula for odds, we have

Odds to lose = (% to lose)/(% to win) = 67%/33% = 2:1

The formula for conversion from odds to percentages is:

% = odds/(1+odds) * 100%

In our case,

% to lose = 2/(1+2) * 100% = 2/3 * 100% = 67%


Case A:
-------
% to win = 33%
% to lose = 67%
$won = $1,000
$lost = $1,000

EV(case A) = 33% * $1,000 - 67% * $1,000
= $330 - $670
= -$340

We lose money, therefore FOLD!

Case B:
-------
% to win = 33%
% to lose = 67%
$won = $2,000
$lost = $1,000

EV(case B) = 33% * $2,000 - 67% * $1,000
= $660 - $670
= -$10

We are about zero, so FOLD or CALL is fine. FOLD is preferred.

Case C:
-------
% to win = 33%
% to lose = 67%
$won = $3,000
$lost = $1,000

EV(case C) = 33% * $3,000 - 67% * $1,000
= $990 - $670
= +$320

We are making money on average. CALL!


To use the odds table I attached, all you need to do is multiply what you HAVE TO CALL with the odds from the table. That gives you the minimum required pot so that you make profit (or fancier said, for you to have positive EV, or +EV).

For example, say that you have an inside str8 and flush draws on the turn. Someone moves all-in, you are last to act and have to determine whether a call is +EV or not.

Your draw has 12 outs, 9 for flush, 4 for str8, but 1 of the cards is counted for both, so the total is 12 outs. There is one card to come. So you look in the table and see that the odds against you are 3:1.

If you have to call $25, for example, then you multiply $25 by 3 which is $75. That is the MINIMUM size of the pot that will make a call +EV.

If the pot is only $60 and you call, your call is -$EV which means you lose money in the long run.

If the pot is $85, for example, you must call since you have odds (which means you have +EV).


I hope this clarified these concepts more than it confused them.

 

[maybull]

Actually, my eyes are starting to uncross...it helps to relate it to odds which is something I am familiar with. Although I started getting confused again near the end when you refer to the odds chart.

Gonna have a shower and come back to it in a bit

Thanks!!