“I’m interested in locating the holy grail of the minimum means to express the most complex ideas.” Ben Nicholson
This is the sixth (and last) in a series of articles introducing my GTO Holy Grail Algorithms. These articles are based on my newest book, Lectures on Poker, Volume 1: Small Stack Tournament Strategy.
If you missed any of my previous articles on the concept, you can find them here:
Short-Stack GTO Play
Reshoving
“Reshove” is an awkward term. It doesn’t refer to shoving over a previous shove, which is more akin to calling the shove. Reshoving means that our hero is jamming over a previous preflop raise. This makes GTO reshove modeling more complex than open-shove modeling.
Suppose Computer Jack opens to 2.5 BBs with the “correct” GTO range. From there, Diane battles Jack (inside the computer) until a Nash equilibrium is established, generating GTO reshoving ranges for Diane and bet-call ranges for Jack. This is the way most GTO solutions are created.
But this is just a model. In a real tournament, Jack isn’t constrained to open to 2.5 BBs, and he’s not constrained to open with a “correct” GTO range. He might GTO-open to 2.1 BBs or he might raise a limper to 3.0 BBs. Or, perhaps, Jack opens with a tighter-than-GTO range. Each situation leads to a different GTO solution.
Furthermore, if Diane’s response to Jack’s shove is non-GTO, Jack’s shoving range might shift again.
Finally, reshoving and folding aren’t Diane’s only options. Suppose Jack opens to 2.2 BBs and Diane is on the button with 20 BBs effective. Diane could just flat and play with superior position. Or she could raise to 6 BBs, perhaps taking down the pot right away. Poker gets more complicated when there is action ahead of us.
Balance the equities
Reshoving against an opener can be analyzed in two basic ways: conventionally and game theoretically. The conventional method utilizes “equities math” to estimate whether we have a +chip EV reshove or not. (Caveat: Chip EV isn’t the only consideration for making a tournament decision.)
First, we estimate the villain’s opening range (OR) and his range for calling our shove (CR). These two ranges determine our fold equity, FE = (1-CR/OR). For example, if the villain calls our reshove with 40% of his opening range, our FE is 60%.
Next, we need to estimate our equity-when-called (EWC), which is the percentage of time we expect to win if we are called. Figure 1 shows the break-even (Zero chip-EV) lines for various values of FE and EWC, assuming a big-blind ante and an open bet of 2.5 BBs. We can see that these break-even curves depend on the size of the effective stacks. When the stacks are small, we need less EWC and FE to break even.
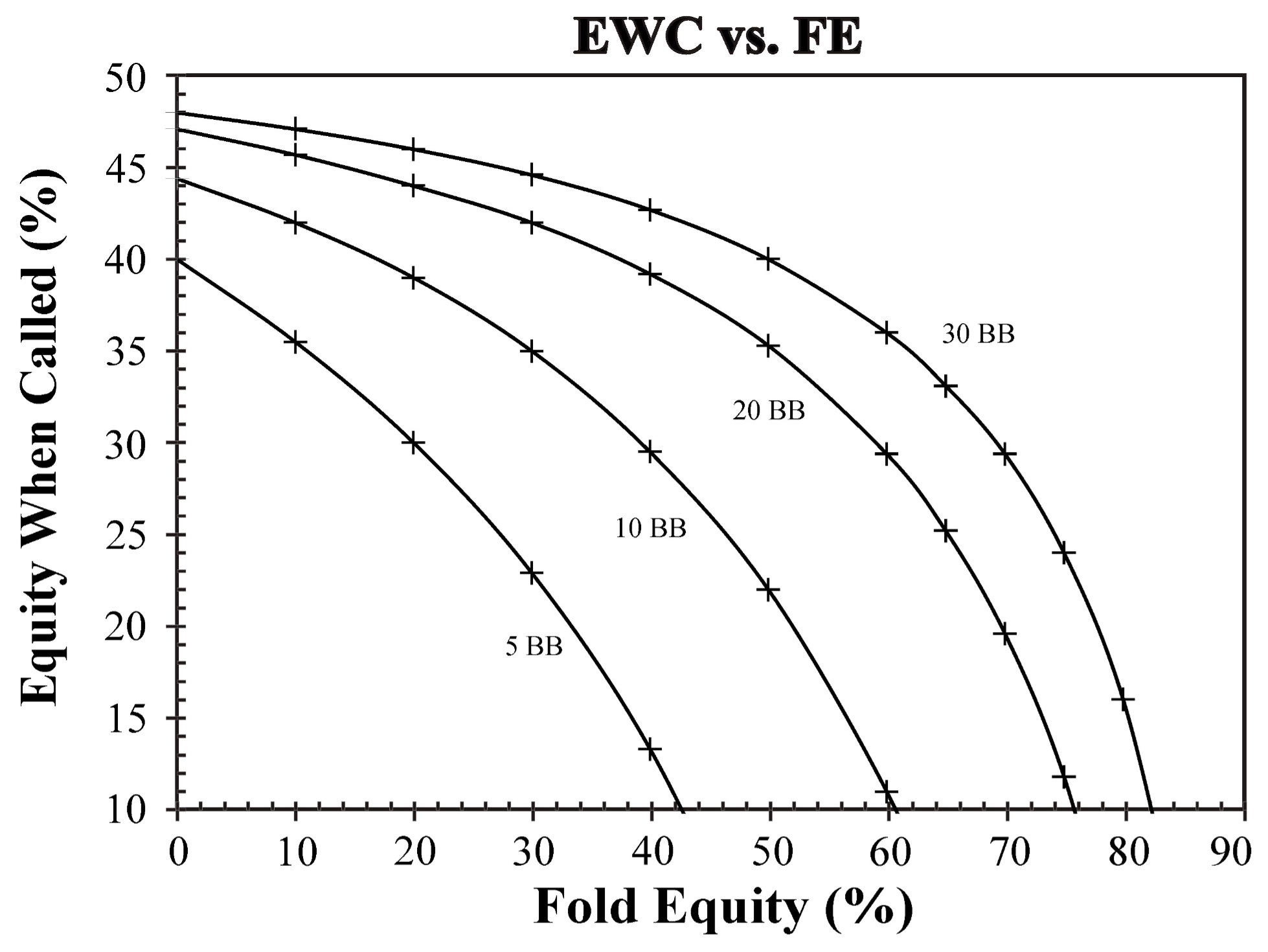
So, when facing a reshove decision, our first question should be what is the villain’s opening range, followed by how often will he fold to my shove? These answers will depend on the villain’s playing personality, the seat he opened from, and our own table image. Once we have these parameters, we can estimate how well our hand will hold up to his calling range (EWC).
If the villain is a loose opener, we don’t need a very strong hand to reshove. He will either fold a large fraction of his openers or we’ll have good EWC when he calls with a wide range. If he opens with a tight range and won’t likely fold to our shove, we need a much stronger hand to reshove.
This is a difficult analysis, especially in a live tournament. But it’s much easier when the stacks are short. For example, with 10 BB stacks we can reshove with nearly any two cards if we expect the villain to fold 40% of the time. And we would need only 44% EWC if he never folds. In fact, these short-stack situations are precisely where game theory can be a powerful tool.
Creating a GTO reshove strategy
We can use ICMIZER3 to determine the GTO reshoving ranges for various initial conditions, just as I did for open shoving in my previous articles. Figure 2 summarizes our reshove ranges from the button after a 2.5 BB open.
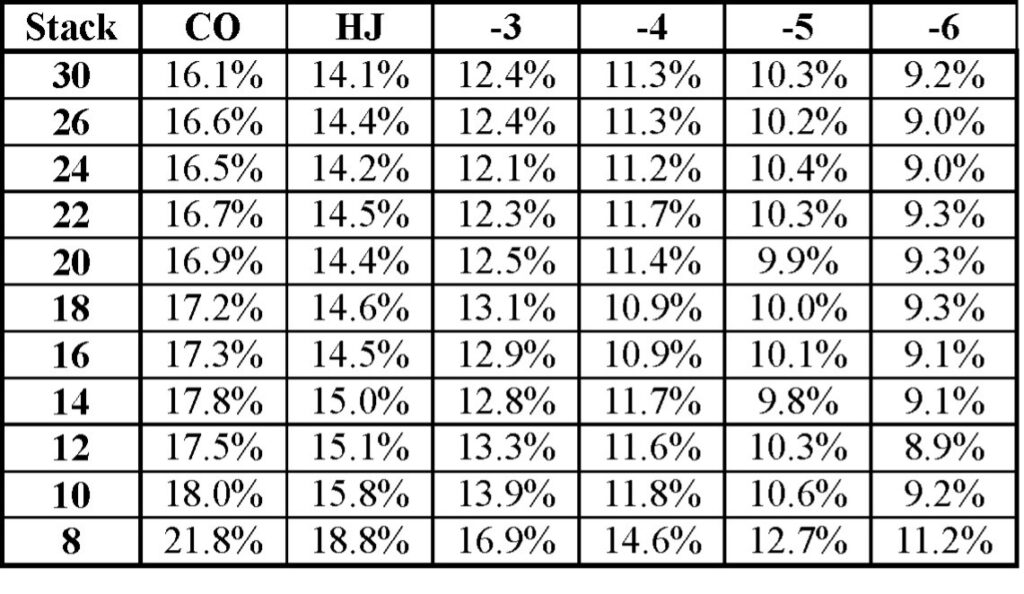
Suppose a player opens to 2.5 BBs from the hijack. We are on the button with 20 BB effective stacks, so our reshoving range would be 14.4%. Notice that our GTO reshoving range tightens as the villain opens earlier, which is what we should expect.
Creating a GTO reshove index
A percent range table is difficult to use in a live game. We would need a separate table for each table position and we would need to know which combos belong to each percentage range. That would be a lot to memorize.
We can make some reasonable approximations, however. Just as we did for our open-shove analysis, we can convert these range percentages to reshoving indexes. Then we simply plot the data, which is shown in Figure 3 for the case when our hero is on the button.
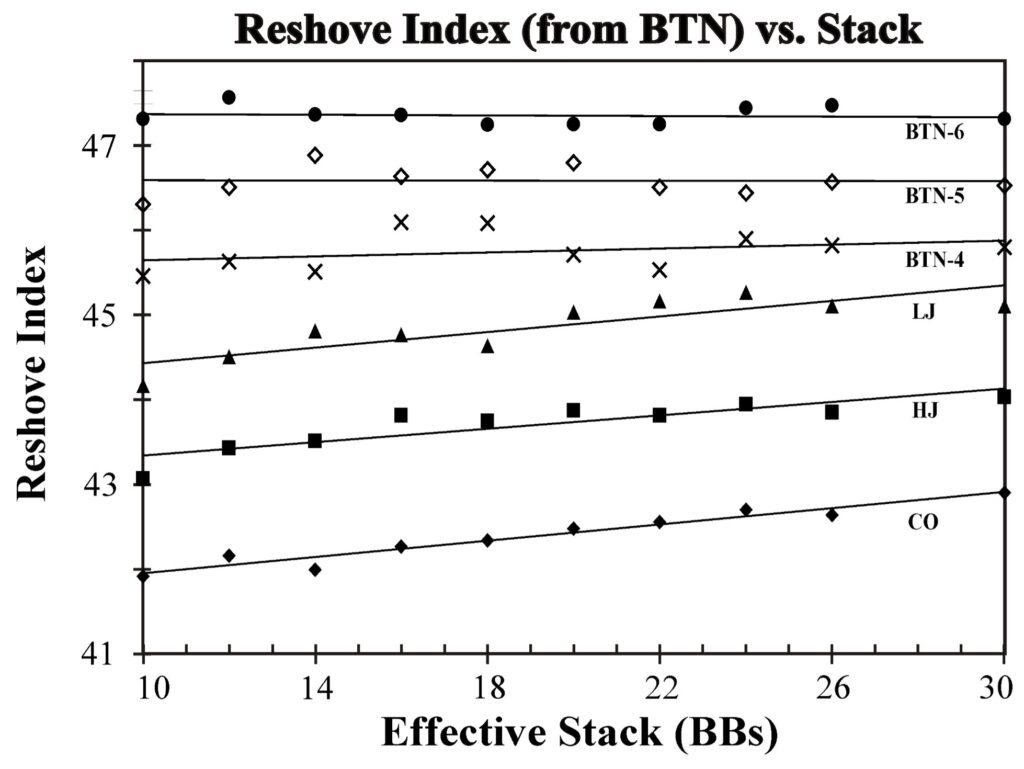
We can see that the slopes of these curves are nearly zero, which means we can characterize each curve with a single number. When we do this for each of hero’s seats, we produce Figure 4. We have now condensed a huge amount of data into a simple chart.
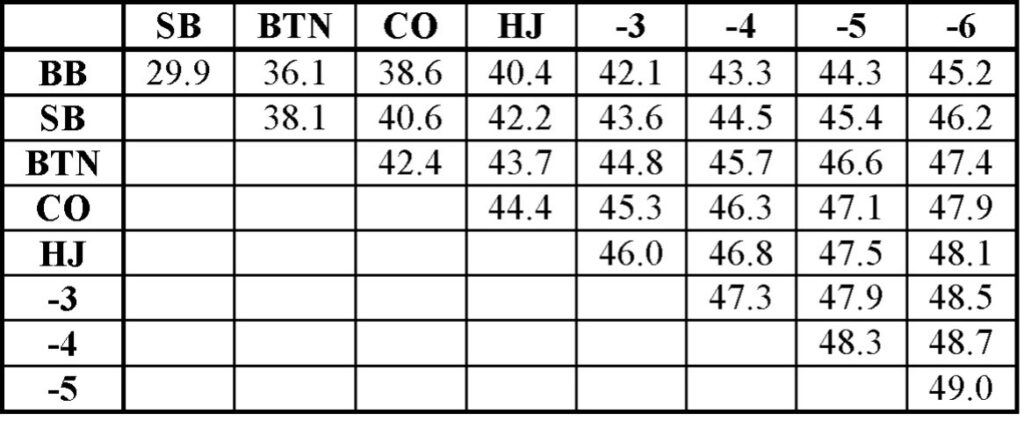
Suppose we’re on the button and the hijack opens to 2.5 BBs; our reshove index would be 43.7 points. If the combo power index of our hand is larger than this, we have a GTO reshove opportunity. A hand such as A♠ 6♠ (34+6+5 = 45 points) would be just strong enough. But if the open came four off the button, our hand would be too weak.
The Holy Grail reshove algorithm
This chart is still difficult to use at the table, but there is another simplification we can make; we simply compare our reshove index to our position index, which we have already memorized from my earlier articles. This leads to the holy grail reshove algorithm:
2.5 BB reshove index (non-blinds) = position index + 14 + R1
2.5 BB Reshove Index (blinds) = position index + 20 + R1
When we’re not in the blinds, we add 14 points to our position index when Mr. Opener is exactly on our right. Then we add one additional point (R1) for every seat farther to the right that he sits. Our reshove algorithm is the same from the blinds, except that we add 20 points instead of 14. That’s it! It’s simple.
I didn’t just pull this algorithm out of thin air. I studied many variations and this was a good fit for the data and easy to memorize. The average “error” when using this algorithm is less than 1 index point in nearly all situations. Furthermore, most errors are conservative, meaning we would be reshoving a bit too tightly. (That’s a good direction in which to err since most players will open more tightly than GTO.)

We now have an algorithm that is easy to remember in a live tournament, summarized in Figure 5. Suppose Mr. Hijack opens to 2.5 BBs and it folds to us on the button. The effective stacks don’t matter. Our reshove index is 43 points (28+14+1). We look down and see A-To, which has a combo power index of 47 points (2×17+10+3). This is an easy GTO reshove if we believe Mr. Hijack is opening with a GTO range.
Adjust to the landscape
This becomes our GTO reshove baseline. Then we make adjustments depending on the lay of the land. First and foremost, we must adjust to the style of Mr. Opener. If he’s significantly tighter than GTO, we might exploit his tightness by reshoving tighter since our fold equity and EWC are both likely to be low.
We can use our GTO open index to estimate this (see Part 5). Suppose Mr. Hijack opens to 2.5 BBs. His GTO open index from the hijack is 32+8 = 40 points, which includes A-3o+, 2-2+, and a few other combos. Do we think this particular villain would open with any ace and any pair? If so, we can make an unexploitable reshove. This is even more attractive when we consider that few villains will call our shove with the correct GTO range.
If we believe villain is opening with a range far from GTO, we can adjust our decision by using a conventional equity balancing analysis.
We can also adjust our reshove range depending on the size of Mr. Opener’s bet or whether he raised a limper. If Mr. Opener’s range is unaffected by a limper, we can be a bit more aggressive in our reshove decision since there’s more money in the pot to win.
Finally, we can adjust our decision when we are in a bubble situation. For example, we might fold if we can fold to the money. Or perhaps we reshove a marginal hand when Mr. Opener is likely afraid of busting on the bubble.
Summary
The GTO Holy Grail Algorithms can be easily implemented at a live table; we just need to memorize Figure 5. Or we can have this image available to look at between hands. We use this information to form a baseline decision with high confidence. Then we adjust our decision to our poker landscape.


