G
glworden
Visionary
Silver Level
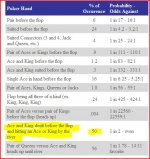
I saw a thread a couple days ago that I just can't seem to find now. One guy said that Cardplayer magazine says the odds of pairing an AK in your hole is 60% by the river. Another guy did some math and said no, it's 50%. I can't find the thread to see how the discussion progressed and what conclusions were drawn. I also can't find this particular scenario in any odds tables.
I come down on the 60% side. I do this with quick approximate odds calculations. In order to pair a hole card, there are six outs and five streets. Six outs per street = about 12%. Add five street possibilities to arrive at 60%.
Now I'll do what I believe to be the actual odds. If I'm doing this wrong, then I've been doing it wrong for ages and somebody needs to set me straight.
Since I only know my two hole cards, I'm looking for one of six outs from a universe of 50 cards on the first street. The probability is therefore 6/50. If I don't hit, I still have 6 outs from a universe of 49 cards so the odds of hitting on the second card of the flop (if I didn't hit the first) is 6/49, and so on.
Adding these probabilities I get:
(6/50) + (6/49) + (6/48) + (6/47) + (6/46) =
.1200 + .1224 + .1250 + .1277 + .1304 = .6255
So, the way I get it, there's a 62.55% chance that you'll pair at least one of your hole cards by the river. If you're all in pre-flop and your opponent shows no ace or king, your chances are even higher since the universe of available cards now starts with 48 rather than 50.
I'm not saying AK has a 62.55% chance of winning. There are odds calculators which show those odds against random hands and against given hands.
If you don't pair a hole card 62.55% of the time by the flop, tell me where I'm wrong, please.
Gary
I come down on the 60% side. I do this with quick approximate odds calculations. In order to pair a hole card, there are six outs and five streets. Six outs per street = about 12%. Add five street possibilities to arrive at 60%.
Now I'll do what I believe to be the actual odds. If I'm doing this wrong, then I've been doing it wrong for ages and somebody needs to set me straight.
Since I only know my two hole cards, I'm looking for one of six outs from a universe of 50 cards on the first street. The probability is therefore 6/50. If I don't hit, I still have 6 outs from a universe of 49 cards so the odds of hitting on the second card of the flop (if I didn't hit the first) is 6/49, and so on.
Adding these probabilities I get:
(6/50) + (6/49) + (6/48) + (6/47) + (6/46) =
.1200 + .1224 + .1250 + .1277 + .1304 = .6255
So, the way I get it, there's a 62.55% chance that you'll pair at least one of your hole cards by the river. If you're all in pre-flop and your opponent shows no ace or king, your chances are even higher since the universe of available cards now starts with 48 rather than 50.
I'm not saying AK has a 62.55% chance of winning. There are odds calculators which show those odds against random hands and against given hands.
If you don't pair a hole card 62.55% of the time by the flop, tell me where I'm wrong, please.
Gary