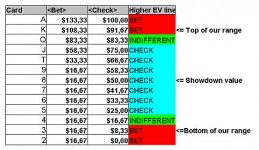
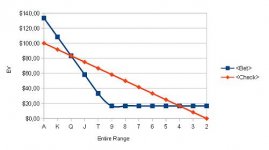
Fknife
Legend
Silver Level
Hello 
This will be the ongoing Study Group thread for Bill Chen's book: "The Mathematics Of Poker".
About the book and the Study Group.
For anyone who hasnt heard about "The Mathematics Of Poker": its a great book! Generally its about...poker math (as the title itself suggests) but it goes a bit deeper, beyond basic stuff (such as: counting outs or calculating pot odds) and presents also some interesting concepts from game theory (mostly by introducing and then solving various "toy-games" which are used to model poker-related "scenarios").
The book consists of 5 parts. We will start from the 1st one, which generally serves as a reminder of some basic concepts such as: Probability, expected value, Variance, Bayes Theorem etc. Its rather boring and does not contain anything revealing but it allows to get used to the "language" of the book and authors' overall approach. Also, if anyone does not know/remember those things - thats your chance to change it
The 2nd part is about "Exploitive Play", which I think is the part that most "poker math" books are all about so I originally prefered to skip it but... we dont have to. The 3rd part is IMO the most interesting one because it deals with the "Optimal Play". Thats the part that Im personally very excited about but...we will talk about it when (and if) we get there.
The 3rd part is IMO the most interesting one because it deals with the "Optimal Play". Thats the part that Im personally very excited about but...we will talk about it when (and if) we get there.
Im aware that the book can be a bit difficult and that not everyone has a lot of spare time for poker, therefore I suggest we start with reading one chapter per week. In the meantime, throw questions (if you have any) or just start a discussion about the current chapter here. After a week, I will try to put a short summary about the crucial concepts from that chapter and we will move on to the next one. You should have access to the book -> I'm not going to transcribe/copy the entire book here. Also, since the book is very theory heavy, I will try to come up with some practical examples. We can adjust the studying speed later, depending on everyone's preferences.
Tbh, I have really high hopes for this thread and I think we can learn lots of interesting things together. Currently, I know of 4 people who already have the book and few others who declared an interest in the Study Group. I will try my best to keep this thread going, unless of course I end up talking to myself here. One more thing: I've never been in any "study group" before so if you have any suggestions (eg: how it should look like), let me know! Also, I created this thread but its not MY thread. You're welcomed to post whatever you like and talk with whoever you want to talk (keeping it on topic ofc ). Good luck and lets have fun!
). Good luck and lets have fun!
Few tips before you begin.
a) Right, so the book can be sometimes a bit difficult, especially to people not used to that kind of technical, math oriented books. Dont hasitate to ask any questions about stuff you dont understand.
b) Do not get discouraged if you dont get everything at the first time. There is no shame in reading a single page (or even a single sentence) few times before moving on (the same goes with going back to previous chapters). Also, sometimes its better to just leave the book and get back to it next day.
c) Some parts (especially the "Optimal Play" one) may look a bit "out of touch with reality" (eg: using a [0, 1] distribution instead of hole cards) and you may not see any correlation between stuff from the book with how it could be applied to the actual game. Well, unfortunatelly (or maybe thats for the better) there is a huge gap between presented concepts and its real-world applications and there is even a lot more work to be done after finishing the book. It does not mean that the book is useless though. I firmly believe that you can learn and improve a lot even if you dont choose to follow the path presented by the book (the next step after finishing it could be: "breaking down" your game in a software such as CardrunnersEV).
d) Finally: do not expect too much out of this book. The amount of work, time and patience you put into understanding it, does not necessary guarantee that you will instantly become a better player and start crushing tough games. Dont set any high goals/expectations, instead just treat it as: a learning experience, another way of looking at a game, a chance to talk with others about interesting concepts/things you dont understand, a chance to improve and learn something new.
Useful resources for the book.
1) Lectures from MIT 15.S50 (aka MIT Poker Class)
Lecture 3: Introduction to Game Theory
Slides : http://web.mit.edu/willma/www/2013lec3.pdf
Video 1: https://www.youtube.com/watch?v=BuxCNZ0RVKA
Video 2: https://www.youtube.com/watch?v=xA6WWSVLitY
Lecture 5: Game Theory in Practice: A Tale of Two Hands
Slides : http://web.mit.edu/willma/www/2013lec5.pdf
Video 1: https://www.youtube.com/watch?v=VHcrsMPQtgo
Video 2: https://www.youtube.com/watch?v=dwtrcee6gNk
2) https://www.youtube.com/user/PokerDavidD/videos
(31 short videos about Game Theory in Poker. They are a bit...slow (the author likes to repeat himself) but its a good start I guess.)
3) Jerrod Ankenman's (co-author of MoP) forum thread about GT in poker
4) http://blog.gtorangebuilder.com/
5) Matthew Janda - "Applications of No-Limit Holdem".
This will be the ongoing Study Group thread for Bill Chen's book: "The Mathematics Of Poker".
About the book and the Study Group.
For anyone who hasnt heard about "The Mathematics Of Poker": its a great book! Generally its about...poker math (as the title itself suggests) but it goes a bit deeper, beyond basic stuff (such as: counting outs or calculating pot odds) and presents also some interesting concepts from game theory (mostly by introducing and then solving various "toy-games" which are used to model poker-related "scenarios").
The book consists of 5 parts. We will start from the 1st one, which generally serves as a reminder of some basic concepts such as: Probability, expected value, Variance, Bayes Theorem etc. Its rather boring and does not contain anything revealing but it allows to get used to the "language" of the book and authors' overall approach. Also, if anyone does not know/remember those things - thats your chance to change it
The 2nd part is about "Exploitive Play", which I think is the part that most "poker math" books are all about so I originally prefered to skip it but... we dont have to.
Im aware that the book can be a bit difficult and that not everyone has a lot of spare time for poker, therefore I suggest we start with reading one chapter per week. In the meantime, throw questions (if you have any) or just start a discussion about the current chapter here. After a week, I will try to put a short summary about the crucial concepts from that chapter and we will move on to the next one. You should have access to the book -> I'm not going to transcribe/copy the entire book here. Also, since the book is very theory heavy, I will try to come up with some practical examples. We can adjust the studying speed later, depending on everyone's preferences.
Tbh, I have really high hopes for this thread and I think we can learn lots of interesting things together. Currently, I know of 4 people who already have the book and few others who declared an interest in the Study Group. I will try my best to keep this thread going, unless of course I end up talking to myself here. One more thing: I've never been in any "study group" before so if you have any suggestions (eg: how it should look like), let me know! Also, I created this thread but its not MY thread. You're welcomed to post whatever you like and talk with whoever you want to talk (keeping it on topic ofc
Few tips before you begin.
a) Right, so the book can be sometimes a bit difficult, especially to people not used to that kind of technical, math oriented books. Dont hasitate to ask any questions about stuff you dont understand.
b) Do not get discouraged if you dont get everything at the first time. There is no shame in reading a single page (or even a single sentence) few times before moving on (the same goes with going back to previous chapters). Also, sometimes its better to just leave the book and get back to it next day.
c) Some parts (especially the "Optimal Play" one) may look a bit "out of touch with reality" (eg: using a [0, 1] distribution instead of hole cards) and you may not see any correlation between stuff from the book with how it could be applied to the actual game. Well, unfortunatelly (or maybe thats for the better) there is a huge gap between presented concepts and its real-world applications and there is even a lot more work to be done after finishing the book. It does not mean that the book is useless though. I firmly believe that you can learn and improve a lot even if you dont choose to follow the path presented by the book (the next step after finishing it could be: "breaking down" your game in a software such as CardrunnersEV).
d) Finally: do not expect too much out of this book. The amount of work, time and patience you put into understanding it, does not necessary guarantee that you will instantly become a better player and start crushing tough games. Dont set any high goals/expectations, instead just treat it as: a learning experience, another way of looking at a game, a chance to talk with others about interesting concepts/things you dont understand, a chance to improve and learn something new.
Useful resources for the book.
1) Lectures from MIT 15.S50 (aka MIT Poker Class)
Lecture 3: Introduction to Game Theory
Slides : http://web.mit.edu/willma/www/2013lec3.pdf
Video 1: https://www.youtube.com/watch?v=BuxCNZ0RVKA
Video 2: https://www.youtube.com/watch?v=xA6WWSVLitY
Lecture 5: Game Theory in Practice: A Tale of Two Hands
Slides : http://web.mit.edu/willma/www/2013lec5.pdf
Video 1: https://www.youtube.com/watch?v=VHcrsMPQtgo
Video 2: https://www.youtube.com/watch?v=dwtrcee6gNk
2) https://www.youtube.com/user/PokerDavidD/videos
(31 short videos about Game Theory in Poker. They are a bit...slow (the author likes to repeat himself) but its a good start I guess.)
3) Jerrod Ankenman's (co-author of MoP) forum thread about GT in poker
4) http://blog.gtorangebuilder.com/
5) Matthew Janda - "Applications of No-Limit Holdem".