28 Steps to big Sunday tournaments.

Yesterday I played in the $215 PS Sunday Warmup, my first big sunday tournament ever. Even though I usually hate donkaments, i actually enjoyed this one, so i'd like to repeat this in future Sundays, but tbh, it's a little bit above proper BR management for me.

So I've decided I'd try funding Sunday tournaments by playing steps SNGs. Step 1 cost $7.5 and Step 4 tickets get you into the $215 tournaments. My record so far in step SNGs is that i bought a single step1 ticket and turned it into the buy-in for yesterday's tournament, so obviously i think they're easy, but 1 may not be much of a sample size.

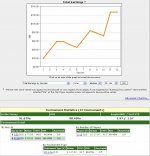
So I've decided to try a little experiment with those. I'll buy into 28 step 1 tournaments for a total of 28x$7.50 = $210, probably 4 or 6-tabling them, and i'll see how many step 4 tickets I can turn these into. Hopefully more than 1. I'll report partial results in this thread while going through this.

Good luck Belgo. it will be intresting to see you roi after the steps, and then also after the tourneys you play. Do you play these the same you would play any sngs? Does your strategy change between each step?

Payout is significantly different from regular SNGs, as top2 move a step up and 3th, 4th and sometimes 5th get another chance at the same level or a step lower. It changes the ICM value of your chips and thefore affects proper push/fold decisions significantly.

Have you tried the 60 FPP turbos? I was thinking of giving that a go - maybe playing 5-10 of them to see if I could do something. They are 100 person sng's that pay like this:

1rst - step 2
2nd-10th - step 1

Good luck with your experiment!

(gonna move this to poker rooms)

Buy-in is too low. It would be massively -EV to play those instead of my usual 100nl. Actually, the step1 are a bit too cheap too, but i think it makes the experiment more interesting to start from those.

Buy-in is too low... In theory it is free as these are points based. -EV.... It would be a free entry into the Sunday Million or Warm-up.

Belgo, I'm really interested to see how this turns out. I literally just had someone limp/call my shove with 86s.

60FPP is not free. It is worth a little under $1.

I win an average of $30/hour playing 100nl, so playing a freeroll instead of my regular games is actually costing me $30/hour, imo. Ergo, I can't afford to play freerolls anymore...

So it would be +EV for me to play them.

Umm... can I buy your book?

Seriously, though, how many hands is that over? Unless you're playing a ton of tables, I don't even see how that's possible. I averaged about that much for a bit, but that was a lucky streak of 10-20k hands. It was much lower in the long run.

3 BB/100 and 500 hands/hour gets you there. 500 hands/hour is between 6 and 9 tables. Only 23k hands so far I admit, but i'm actually running at 4 BB/100 with rakeback, so i think 3 BB/100 is reasonable in the longer run.

Just out of curiousity, would you say that any particular time of day is easier on these step tournaments? I have a couple of Step 2 tickets and have been putting off playing with them. The equivalent of $27 is far more than I have paid before to play any game/SnG/tournament so I want to try to maximize my chances.

no idea. Just play when YOU feel best.

Also, try to play when i'm not at the tables...

Update after day 1: played 4 step1 tournaments for 4x$7.50 = $30. Won 3 step2 tickets (top 2 finish) and 1 step1 ticket (3rd) out of it. Those 4 tickets are worth $88.50, so a nice $58.50 profit in step equity.

Obviously got lucky and ran above expectation, but the standard of play was really bad. Mostly people call too light near the bubble when the payout structure makes it clearly -$EV.

Played another 4 step1 sngs tonight (4-tabling). Bought in cash for 3 of them for $22.5 dollars and used the step1 ticket i won yesterday for the 4th one.

I won 2 step2 tickets, got 4th place for $1.5 back and 6th for nothing. That's worth 2x$27+1.5 = $55.5, or a $25.5 benefit over the $30 worth of buy-ins. That makes the following balance at end of day 2:

Buy-ins: 7 step1 = $52.50
Current worth: 5 step2 tickets + $1.5 = $136.5

this is pretty bawler, i might try to convert my FPPs and grind this ish since it seems pretty +EV

Awesome.

I would try it as well, if I had any money left on stars, and if I was interested in playing the million or warmup. Maybe in the future, or like once to see if I can get to the warmup and wouldn't mind playing it once.

Well, i'm on a heater obviously and i don't really expect these results to extrapolate and that i'll get 20 step2 tickets out of my scheduled 28 step1 buy-ins. Also, steps 2 and 3 should be a bit harder to beat i guess. But yeah, it seems reasonably +EV.

This is partly translated from a French site: http://www.clubpoker.net/forum-poker...-2-t64429.html

Let's call a the $ value of a step1 ; b the value of a step2 and c the value of a step3.

Step 3 gives 2 tickets to 215$ tournaments and requalifies 3 players to another step3. So we can compute the value c of the step3 as

9c = 2*215 + 3c
6c = 430
c = 430/6= 71.67$ (instead of $82)

A step2 gives 2 tickets to step3 ; 2 tickets to step2 and 1 ticket step1, i.e.

9b = 2c+2b+a
7b=143.33+a (1)

Finally, a step1 gives 2 tickets to step2; 1 ticket to step 1 et 1.50$, so

9a = 2b + a + 1.50
8a = 2b + 1.50 (2)

So we have a system of 2 equations (1) and (2) with two unknows that we can solve and get

b = 21.26$ (instead of $27)
a = 5.503$ (instead of $7.5)

So when you buy-in for $7.50 in a step1 with the intention of using step4 tickets for $215 tournaments, you are effectively playing a $5.5+2 tournament, not a $7+0.5 as advertised. That's a hell of a lot of rake, tbh.

On the other hand, you have a similar cumulative effect for ROI while moving up the steps, which should compensate this. But it's worth noting that for the average player with no edge or the bad player with a negative edge, these steps are a complete rip-off.

Tonight i started using my step2 tickets and so i mixed two step1 for which i bought in for 2x$7.5=$15 and 2 step2 for which i bought in with tickets worth 2x$27=$54 for a total buy-in of $69.

I bubbled both step1 in 4th place and got $1.5 back for each. In the first step2, I got 4th which gives me back a step2 ticket worth $27 and in the other one i won a step3 ticket worth $82. This makes a total of $82+27+3=$112 or a $43 profit for this session.

Played another 4 step1 sngs tonight (4-tabling). Bought in cash for 3 of them for $22.5 dollars and used the step1 ticket i won yesterday for the 4th one.

Overall balance is as follows:

Buy-ins: 9 step1 = $67.50
Current worth: 1 step3 ticket (82) + 4 step2 tickets (27) + $4.5 = $194.5

A graphical view of the 12 steps i played so far.

Also should mention that these require about 40 minutes to complete and I 4-table them, so this is 2 hours of play overall.

Attached Images

steps.jpg (117.7 KB, 13 views)

What program is that?

it's a web site. http://www.pokerdominator.com. I started using it before i got serious and bought pokertracker and holdem manager, and still use it nowadays to keep track of overall sessions.

Ah ok

Gonna give a couple more of these a go, tried 2 but was not running hot while I played them, going to do a couple tonight while im in good spirits

Your best bet is the $8.80+R turbo sats on Sunday mornings. Pretty easy to get in for a relatively small investment.

I remember using that site before I got serious
I tried to keep it up but my $20 bankroll died too quickly
I also seem to remember using it for keeping track of my playmoney sessions lol.

this is kool. i hope u win some step 4 tickets

Ha ha! And with all the hands that eNTy posts, I'm guessing he can improve his bb/100 by leaving his computer off and lighting a euro or two on fire every hour.

What does this.

Have to do with this ?

Are you saying I'm bad ?

Also, when you win gratuitous amounts of money in the Warmup you will have paid for your lack of playing 100nl.

Meta-game imo

Pretty sure playing the warmup is +ev. Just want to figure out the best way to pay for the $215 buy-in time-wise. Could be playing 100nl which would require about 7 hours. Could be playing steps, and this experiment is supposed to give me an idea of the time and $$ it requires per ticket. One thing i'm pretty sure of is that it's not through 60FPP freerolls with step2 prizes, though.

warm-up > milli because it starts earlier!

Fired up another 4 steps today. 2 step1 that i bought in for $15, as well as a step2 and a step3 that i bought in with tickets. In total, that's $124 worth of buy-in.

Won the step3, got 3rd in the step2 which gives me a step2 ticket back, won a step1 and lost the other. In total, that's 2 step2 tickets and a step4 for a total return of $215+2x$27 = $269 , i.e. a profit of $145.

Overall balance is as follows:

Buy-ins: 11 step1 = $82.50
Current worth: 1 step4 ticket ($215) + 5 step2 tickets ($27) + $4.5 = $354.5
Current profit: $272

keep going BS still following ya...I think once I get another bigger BR going I will try this same procedure

ya good luck belgo, hope you make it.